Fuerzas
La primera de ellas es la cuadrada hueca, la segunda la doble T ( también llamada H) , la tercera la T y la cuarta la L. Hay muchas otras, pero quizás estas son las mas usadas de todas.
Si tenemos soportar un peso en el centro de un puente de 1000 Kg, y el puente está apoyado por dos pilares, ¿Qué esfuerzo soporta cada pilar?.
Respuesta: Como el peso dista lo mismo de cada pilar y como hay dos, el esfuerzo en cada uno es 500 kg.
Veremos otras situaciones un poco mas complicadas.
Ejercicio:
Calcular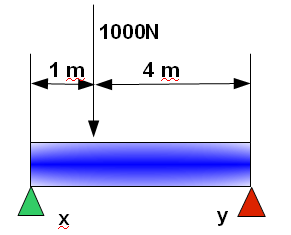 que esfuerzo soporta el apoyo X y el apoyo Y si la fuerza de 1000 Nw está a 1 metros de X.
que esfuerzo soporta el apoyo X y el apoyo Y si la fuerza de 1000 Nw está a 1 metros de X.
 que esfuerzo soporta el apoyo X y el apoyo Y si la fuerza de 1000 Nw está a 1 metros de X.
que esfuerzo soporta el apoyo X y el apoyo Y si la fuerza de 1000 Nw está a 1 metros de X.
a) Se cumple que las fuerzas hacia arriba son iguales que las fuerzas hacia abajo y por tanto, 1000 = Fx + Fy
b) Si quitamos el punto de apoyo X, entonces la barra se caería por la izquierda. Tenemos que sujetarla para que no se caiga. Si la sujetamos justo debajo de la fuerza de 1000 Nw, la fuerza necesaria para evitar que se caiga sería también de 1000 Nw. Si nos alejamos del punto a la izquierda vemos que la fuerza que tenemos que emplear decrece. Esto es , a mas lejos, menos fuerza para evitar que se caiga. Por tanto, y aplicando la ley de la palanca, tenemos que:
Pero como nos hemos desplazado 1 metro a la izquierda, el punto Y también va a trabajar, y por tanto tenemos que hacer de nuevo los cálculos para este punto. Bueno, como dijimos al principio que la suma de las fuerzas es 1000 tenemos que Fy va a ser 200 Nw, pero sería bueno que hagáis los cálculos para comprobarlo.
Ejercicio 2:
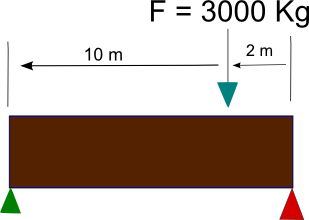 Ejercicio 2.Calcular como se reparten el peso los puntos verde y rojo de la imagen.
Ejercicio 2.Calcular como se reparten el peso los puntos verde y rojo de la imagen.Ejercico 3:
 Ejercicio 3. Calcular el peso que recae sobre los apoyos si las fuerzas que actúan sobre la barra son 100 y 200 Kg.
Ejercicio 3. Calcular el peso que recae sobre los apoyos si las fuerzas que actúan sobre la barra son 100 y 200 Kg.